Quelques exercices pour se réveiller ...
Exercice 1
Représentez logiquement, avec le symbolisme PERT, les données de chacune des assertions suivantes :
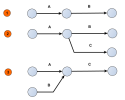
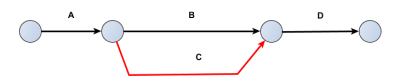
La tâche B ne peut commencer que lorsque la tâche A est entièrement terminée.
Les tâches B et C ne peuvent commencer que si la tâche A est terminée.
La tâche C ne peut commencer que lorsque les tâches A et B sont toutes deux terminées.
Question
Il existe plusieurs solutions
Solution
Exemple : Autre solution :
En pure logique, la solution ci-dessous est également valable.
Mais comme l'identifiant d'une tâche est lui-même formé par le couple des identifiants de ses étapes début et fin [du genre (i,j)], je préfère toujours, au moment du dessin manuel des graphes, éviter d'avoir des tâches parallèles avec des identifiants identiques, car j'aurai inévitablement à les séparer au moment de la saisie, pour ne pas créer des doublons .
Mais, en toute rigueur, l'énoncé 2 ne précise pas que l'état "fin de la tâche C" est identique à l'état "fin de la tâche B", ce qui serait de nature à remettre en question l'intérêt pour le projet de les conserver toutes les deux. Donc, il n' y a a priori pas de raison de fusionner leurs étapes de fin.
Commentaire similaire pour les étapes début de A et B (énoncé 3).
Exercice 2
Dessiner le réseau PERT correspondant à la table de tâches ci-dessous :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | |
C | A, B |
D | B |
Exercice 3
Dessiner le réseau PERT correspondant à la table de tâches ci-dessous :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | A |
C | A |
D | B, C |
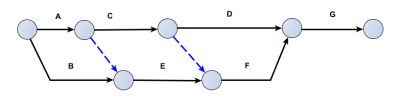
Solution
Exemple : Autre solution :
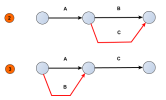
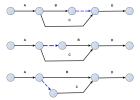
A cause de la contrainte sur l'absence de tâches en double (deux tâches ne peuvent pas être identifiées par le même couple d'étapes début et fin), la construction de ce graphe PERT nécessite l'utilisation d'une tâche fictive.
Comme cette tâche fictive ne sert qu'à rajouter une étape intermédiaire pour que les tâches B et C n'aient plus les mêmes identifiants, il s'avère qu'elle peut indifféremment, pour ce cas précis, être placée à l'un des 4 emplacements suivants : au début de B, à la fin de B, au début de C ou à la fin de C.
En conséquence, les trois graphes PERT suivants sont des réponses possibles tout à fait appropriées pour traduire les mêmes relations d'antécédence.
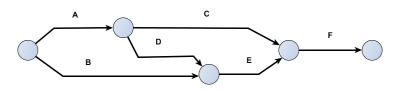
Exercice 4
Dessiner le réseau PERT correspondant à la table de tâches ci-dessous :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | - |
C | A |
D | A |
E | D, B |
F | C, E |
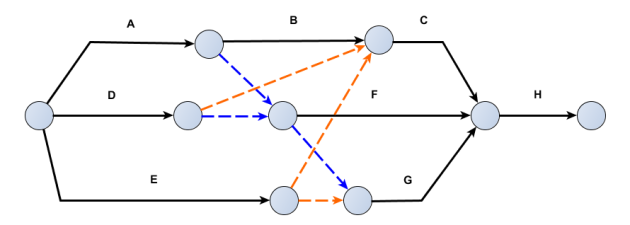
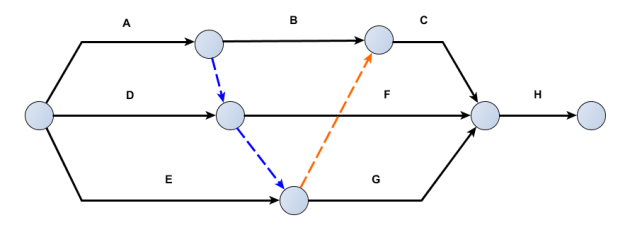
Exercice 5
Dessiner le réseau PERT correspondant à la table de tâches ci-dessous :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | A |
C | A |
D | B, C |
E | B, C |
F | D, E |
Exercice 6
Dessiner, si possible sans fictive, le réseau PERT correspondant à la table de tâches ci-dessous :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | A |
C | B |
D | C, G |
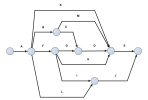
E | D, H, K, M |
F | A |
G | F |
H | F |
I | F |
J | I, L |
K | A |
L | A |
M | B |
Exercice 7
Représentez dans un réseau PERT sans aucune tâche fictive les tâches liées par les contraintes suivantes :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | A |
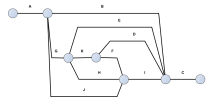
C | B, D, G, I, E |
D | A, G, K |
E | G |
F | K |
G | A |
H | G |
I | A, F ,H, J, K |
J | A |
K | G |
Exercice 8
Représentez en PERT les tâches liées par les contraintes suivantes :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | - |
C | A |
D | C |
E | A, B |
F | C, E |
G | D, F |
Exercice 9
Dessinez le réseau PERT suivant :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | - |
C | - |
D | A |
E | B |
F | C |
G | D |
H | A, E |
I | B, F |
J | G, H, I |
Exercice 10
Dessinez le réseau PERT suivant :
Question
Tâches | Prédécesseurs |
|---|---|
A | - |
B | A |
C | B |
D | - |
E | - |
F | A, D |
G | D, E |
H | C, F, G |
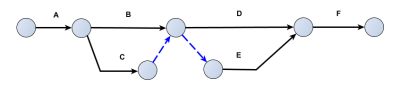
Solution
Exemple : Une solution :
A un moment de la construction du graphe, pour dessiner G qui ne dépend que de D et E, vous avez dû dédoubler l'étape qui liait D (comme étape fin) et F (comme étape début, laquelle recevait la contrainte de la fin de A), de façon à pouvoir établir la contrainte unique de la fin de D sur le début de G. Sinon, c'est la fin de A qui risquait de contraindre le début de G, ce qui ne correspond pas à la logique de ce projet.
Exercice 11
Pas de tableau mais une analyse :
Question
" ... sur ce point, notre contrat prévoit la fourniture de 6 lots d'équipements standard ... bon, je simplifie pour que vous compreniez mieux : la production de chaque lot consiste en une première opération de fabrication suivie d'un test d'endurance ... ah oui, les fabrications des 6 lots ont déjà toutes commencé, on vous a pas attendu ... on pourra expédier dès que le dernier test sera terminé vu que tout part dans le même container ... pour des raisons techniques, les tests des lots 4 à 6 nécessitent chacun qu'on ait fabriqué les trois premiers lots ... "
Solution
Exemple : Une solution
Commentaire :
Contraindre le début du test de chacun des lots 4 à 6 par la fin de la fabrication de chacun des lots 1 à 3 nécessite le tracé de 9 tâches fictives (= 3 x 3). Notre planning PERT risque de devenir rapidement illisible.
En créant une étape de regroupement, nous identifions et mettons en évidence un état particulier du projet qui a pour contenu caractéristique "fin de la fabrication des lots 1 à 3". Ce pourrait en outre très bien constituer un point de visibilité (ou jalon) intéressant pour le projet et son reporting, bien que cela n'ait pas été exprimé par l'équipe projet (voir énoncé).
Ce regroupement des fins de tâches effectué, il ne reste alors plus qu'à contraindre chaque début de test des lots 4 à 6 par cet état intermédiaire pour que notre réseau soit complet.
Chacune des trois tâches fictives de la partie haute du graphique transmet à l'étape de regroupement et ses successeurs une contrainte du type "intervient après la fabrication du lot n" (n variant de 1 à 3).
Par contre, dans la partie basse du graphique, chacune des trois tâches fictives issues de notre étape de regroupement transporte une contrainte du type "intervient après la fabrication des lots 1 à 3", ce qui est beaucoup plus riche d'informations et permet d'économiser des tâches fictives pour alléger le dessin.
Les étapes de regroupement sont également efficaces lorsqu'il s'agit de limiter le nombre d'interfaces entre sous-réseaux du même planning PERT.
Question
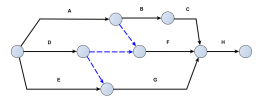
Mettre à jour le réseau PERT ci-dessus avec les informations suivantes :
G dépend aussi de A.
C dépend aussi de D et E.
Solution
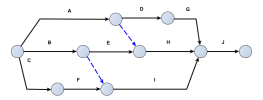
Exemple : Une solution
Commentaire :
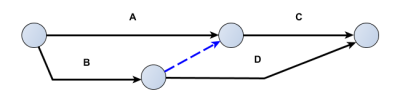
Pour que G dépende de A, il suffit d'un nouvelle tâche fictive entre la fin de A et le début de G.
Pour que C dépende de D, c'est la même chose : une nouvelle tâche fictive entre la fin de D et le début de C fait l'affaire.
Pour que C dépende de E, c'est différent tant que la même étape sert de fin à E et de début à G tout en supportant la contrainte "après la fin de D" apportée par une tâche fictive placée entre D et G. Il faut donc dédoubler la fin de E et le début de G en les maintenant liées au moyen d'une nouvelle tâche fictive. Puis une tâche fictive supplémentaire entre la fin de E et le début de C répondra au besoin.
L'étape début de F est déplacée vers la droite afin de permettre la liaison droite entre la fin de E et le début de C.
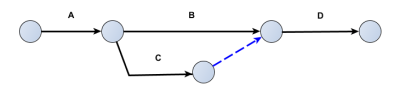
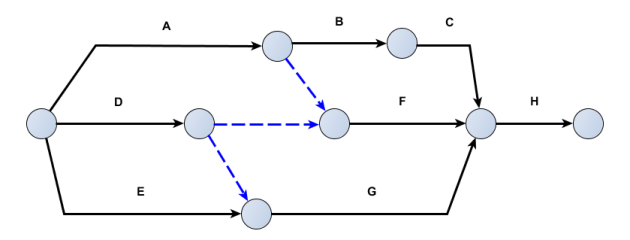
Mais cet exercice de mise à jour de planning admet une autre solution avec le diagramme PERT suivant.
La contrainte de la fin de D sur le début de C est alors transmise via les deux fictives en série et G dépend bien de A, D et E. Même si ce graphe permet l'économie d'une tâche fictive, il risque d'être moins explicite au sujet de la relation d'antécédence existant entre D et C.
Ce dernier graphe n'est toujours pas optimisé dans la mesure où la plupart des fictives ne transmettent qu'une seule contrainte à la fois. Examinons, s'il ne serait pas possible de transmettre dans la même fictive l'information "après la fin de plusieurs tâches prédécesseurs" au lieu de "après la fin de une seule tâche prédécesseur".
On voit par exemple que F et G sont toutes deux conditionnées par la fin de A et D. Un regroupement sur une même étape de la fin de A et de D permettrait de faire passer plus d'information par toute tâche fictive allant de cette étape aux étapes début de F et G.
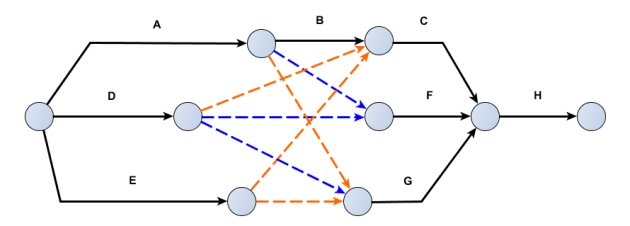
C'est ce qu'on obtient avec le réseau PERT suivant, qui est déjà considérablement allégé par rapport aux deux précédents :
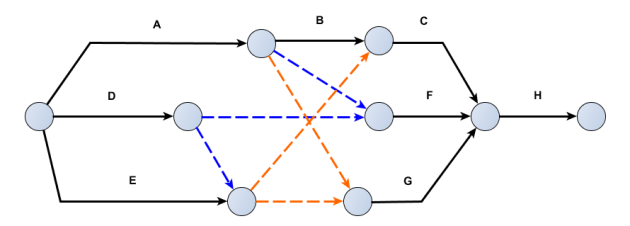
Si l'on n'est pas gêné de faire figurer une contrainte redondante ("C dépend de A" via les 3 fictives en série alors que C dépend déjà de A via B), on peut encore simplifier avec le diagramme PERT ci-dessous, lequel répond complètement aux contraintes exprimées entre les tâches :
La tâche fictive qui servait à contraindre le début de G par la fin de E a été supprimée pour cause d'inutilité. Par voie de conséquence, la tâche fictive contraignant le début de F par les fins de A et D a subi le même sort.
C'est probablement le réseau PERT auquel on parviendrait directement en refaisant sa construction à partir de la table d'origine des prédécesseurs (telle que fournie pour l'exercice n°10) complétée avec les dernières informations prises en compte.
Tâches | Prédécesseurs |
|---|---|
A | - |
B | A |
C | B, D, E |
D | - |
E | - |
F | A, D |
G | D, E, A |
H | C, F, G |