Dessiner un réseau PERT
Exemple : Méthode PERT
Voici l'exemple d'un réseau PERT. Il est composé de 4 tâches. Dans ce cas simple de tâches en série, 5 étapes ont été nécessaires pour le définir.
La forme de ce graphe et sa longueur sur l'axe horizontal sont indépendantes du temps.
C'est l'intérêt principal de ce type de graphe : que le projet démarre en début ou en fin d'année, qu'il prenne du retard ou pas, le graphe est toujours le même !
Pour dessiner le réseau PERT, on utilise généralement les symboles suivants :
ÉTAPE : figure fermée (rond, ovale, rectangle) à laquelle est associée un code alphanumérique qui sert d'identifiant.
L'étape représente le début ou la fin d'une tâche.
TACHE : représentée par un vecteur reliant l'étape début et l'étape fin.
Chaque tâche est identifiée par le couple des codes alphanumériques de ses étapes de début et de fin.
On verra plus loin qu'une tâche possède de nombreuses autres propriétés (libellé, durée, responsable, calendrier, etc.)
Autre représentation (avec GanttProject) :
D'autres méthodes ont été développées à partir de l'autre convention possible : c'est ainsi que la méthode des potentiels représente un réseau dans lequel les tâches sont les sommets du graphe et les arcs les relations qu'elles ont entre elles.
Les tâches sont généralement représentées sous la forme d'un rectangle dans lequel sont insérées des informations (libellé, durée, dates, marges, ressources, coûts, etc.).
Les arcs qui relient certaines tâches entre elles expriment ici la relation d'antécédence qui les ordonne deux à deux.
Le réseau est alors l'ensemble de toutes les tâches ordonnées entre elles.
Concernant le temps, la forme et les dimensions de ce graphe sont également indépendantes de la durée des tâches et du projet.
C'est l'immense avantage des plannings par réseau par rapport aux plannings de GANTT.
Définition : Dessiner
Pour dessiner le réseau PERT, on utilise généralement les symboles suivants :
ÉTAPE : figure fermée (rond, ovale, rectangle) à laquelle est associée un code alphanumérique qui sert d'identifiant.
L'étape représente le début ou la fin d'une tâche.
TACHE : représentée par un vecteur reliant l'étape début et l'étape fin.
Chaque tâche est identifiée par le couple des codes alphanumériques de ses étapes de début et de fin.
On verra plus loin qu'une tâche possède de nombreuses autres propriétés (libellé, durée, responsable, calendrier, etc.)
La tâche PERT
Avec flêche
Une tâche se représente par un vecteur reliant son étape début et son étape fin.
Dans cette représentation, l'arc, de type vecteur, est orienté : le point de départ de l'arc représente le début de la tâche (ici à gauche), son extrémité flèchée représentant l'étape fin de la tâche (celle de droite).
Cette utilisation d'un arc orienté au moyen d'une flèche garantit la distinction entre les deux étapes de début et de fin, quelle que soit la forme de l'arc et les positions relatives des deux étapes entre elles. Impossible de se tromper sur le début et la fin.
Soit maintenant la convention suivante : l'étape fin est toujours représentée plus à droite que l'étape début.
Avec cette nouvelle convention, l'orientation de l'arc devient inutile et sa représentation par un simple trait (au lieu d'une flèche) devient suffisante.
Sans flèche

Cette convention ne fait qu'exprimer, sans le représenter par un axe, que le temps s'écoule de la gauche du graphique vers sa droite.
Comme conséquence de cette convention : le début du projet (premières tâches) sera situé tout à gauche du graphique et la fin du projet, avec les dernières tâches, tout à droite.
Quelques règles :
La règle de dépendance
On l'a vu, la méthode PERT exprime entre les sommets du graphe des relations du type : le sommet Si et le sommet Sj sont en relation s'il existe une tâche permettant de faire passer le projet de l'état défini par Si à l'état défini par Sj.
L'ensemble des tâches d'un projet sera donc l'ensemble des tâches qui font passer progressivement le projet d'un état "début initial" à un état "fin complète".
Chacune des étapes de début et de fin d'une même tâche peut aussi être vue comme un des états intermédiaires du projet, la tâche en question étant le traitement élémentaire ou l'opération qui fait passer le projet de l'état "du début de la tâche" à l'état "de la fin de la tâche".
De ce fait, de nombreuses étapes, vues chacune comme un état défini et prévisible du projet, se trouvent être à la fois des étapes de début de tâches et/ou des étapes de fin de tâches différentes.
Soit deux tâches T1 et T2 avec les caractéristiques particulières suivantes : T1 est la tâche qui fait passer le projet de l'état i à l'état j, T2 la tâche qui fait passer le projet de l'état j à l'état k. On peut les représenter comme suit :
Le dessin ci-dessus traduit alors la réalité suivante : la tâche T2 ne peut commencer que lorsque la tâche T1 est entièrement terminée.
Ce qui peut aussi être exprimé par : la tâche T1 doit être entièrement terminée pour que la tâche T2 puisse débuter.
Remarque : les mots "puisse" et "doit" ont une signification importante dans ces formulations. Mais ils ne font qu'exprimer un fait technique à savoir que les résultats de la tâche T1 sont nécessaires au démarrage de la tâche T2 (contrainte logique en vertu du contexte du projet résultant par exemple d'un choix, d'une obligation ou de tout autre considération susceptible d'expliquer et justifier que T2 débutera après la fin complète de T1 et pas avant). A lire aussi comme "à la fin de T1, les conditions du démarrage de T2 sont réunies". Et cela ne veut rien dire d'autre, surtout pas que la tâche T2 commence dès la fin de T1.
En termes de vocabulaire, on dit que T2 est le successeur de T1 et, par symétrie, que T1 est le prédécesseur de T2.
On dira aussi que T1 et T2 sont en série.
Quelques exemples
Exemple : Représentation logique
Les schémas suivants traduisent les séquences les plus fréquemment rencontrées :
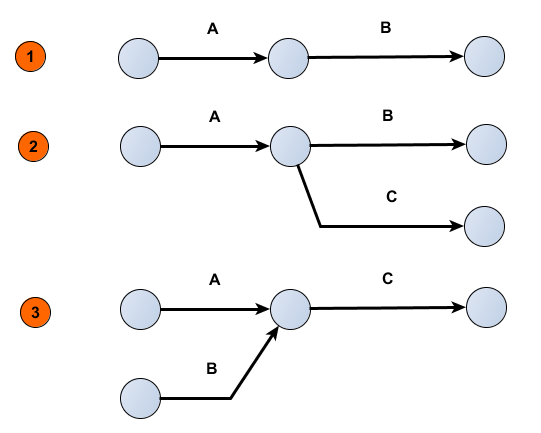
Ligne 1 : la tâche B ne peut commencer que si la tâche A est entièrement terminée.
Ligne 2 : les tâches B et C ne peuvent commencer qui si la tâche A est entièrement terminée.
Ligne 3 : la tâche C ne peut commencer qui si les tâches A et B sont entièrement terminées.
Exemple : Tableaux d'ordonnancement de tâches
Il est fréquent de rencontrer une représentation de l'enchaînement des tâches sous forme d'un tableau à deux colonnes.
En première colonne sont fournis des codes de tâches (A, B, C, T1, T2, T3, ...) et en seconde colonne, pour chaque tâche mentionnée en colonne 1, la liste des tâches qu'elle a comme prédécesseurs (ou comme successeurs selon la convention adoptée).
Pour la même finalité, il arrive aussi qu'un tel tableau contienne trois colonnes organisées comme suit :
colonne 1 : prédécesseur(s) de la tâche.
colonne 2 : codes des tâches du réseau.
colonne 3 : successeur(s) de la tâche.
Tâches | Prédécesseurs |
|---|---|
A | - |
B | A |
C | B |
D | C, G |
E | D, H, K, M |
F | A |
G | F |
H | F |
I | F |
J | I, L |
K | A |
L | A |
M | B |
Ces tableaux de tâches et de relations d'antécédence sont d'un intérêt très limité : on ne les trouve en effet utilisés que pour les exercices pratiques destinés à familiariser les étudiants avec les rudiments du PERT.
La raison est en toute simple : ces tableaux ne sont pas utilisés dans l'élaboration d'un planning PERT, tout au plus en sont-ils un résultat de son traitement.
La tâche fictive
Le symbolisme du PERT, on l'a vu ensemble, n'offre que deux outils pour représenter la logique des projets : des étapes (cercles) et des tâches (arcs).
Mais armé des seules tâches et étapes, le planificateur aura tôt fait de rencontrer une configuration de dépendances logiques entre tâches qu'il sera dans l'impossibilité de représenter graphiquement.
Examinons cela au moyen d'un exemple basique.
Soit les trois tâches suivantes :
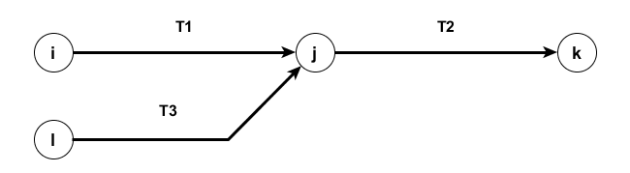
Lors d'une mise à jour du planning, le planificateur doit créer une tâche T4 telle qu'elle n'ait que T3 comme prédécesseur. Comment s'y prend-il ?
Tout d'abord, il conserve T1 et T2 comme elles sont, puis redessine T3 (identifiée par son couple d'étapes (l,j) ) avec une étape de fin pour elle toute seule (m). T3 devient (l,m). Il ajoute ensuite T4 (m,n) comme successeur direct de T3.
Mais, à ce stade, la logique initiale du réseau a été modifiée : en effet, T2 n'a plus T3 comme prédécesseur !
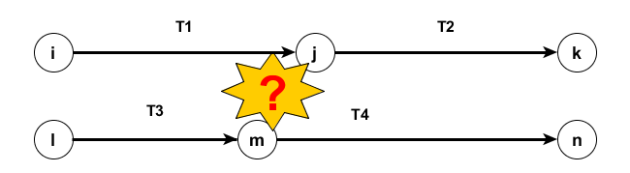
Pour respecter la logique initiale, il faudrait que l'étape j (définie comme "état du projet après la fin de la tâche T1") intègre également l'état du projet tel que défini par la nouvelle étape m, après total achèvement de la tâche T3 .
PERT oblige, on a inventé la "tâche fictive" dont la fonction est de lier deux étapes par une relation "instantanée" pour transférer à l'identique les caractéristiques de l'état du projet. De par sa nature de liaison logique entre deux étapes, c'est bien une tâche comme les autres, mais sa durée est zéro et elle ne consomme pas de moyens.
On la représente sous la forme d'un trait en tirets pour lequel on a maintenu l'extrémité fléchée qui oriente l'arc de son étape début vers son étape fin. Simplement pour que la fictive puisse être tracée verticalement sans ambiguïté sur son orientation. La colorer en bleu met de la couleur dans les graphes PERT, mais ce n'est qu'une convention locale.
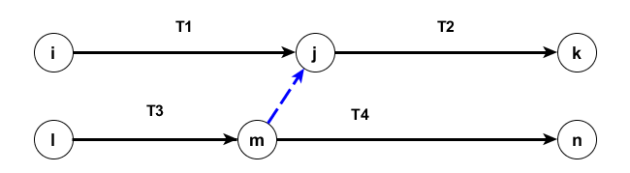
La tâche fictive, identifiée comme toute tâche du graphe par son couple d'étapes début et fin (m,j), transmet sans aucun délai de m à j l'état du projet caractéristique de la fin complète de T3.
Il résulte de la règle de dépendance vue précédemment que T2 ne peut commencer que si la tâche fictive (m,j) est entièrement terminée. Or la fictive (m,j) ne peut elle-même déjà commencer que si T3 est entièrement terminée. Par transition, T2 ne peut commencer que si T3 est entièrement terminée, ce qui constitue la logique d'enchaînement du départ que nous devions préserver lors de la mise à jour du graphe PERT.
Remarque :
Remarque : ainsi définie, notre tâche fictive n'est rien d'autre qu'une relation d'antécédence de la méthode des potentiels. Mais, à la différence de cette dernière qui concerne des tâches (en leur qualité de sommets du graphe), la fictive PERT pose une relation entre deux étapes, étapes qui représentent les sommets du graphe PERT. Bien entendu, la fictive n'a pas cours dans la méthode des potentiels, c'est pour cela qu'on n'en rencontre jamais dans les outils standard de gestion de projet.



